LATIHAN SOAL TENTANG FUNGSI EKSPONENSIAL DAN LOGARITMA ~ MEDIA PEMBELAJARAN BERBASIS BLOG FARAH FABIOLA

LATIHAN SOAL FUNGSI EKSPONENSIAL DAN LOGARITMA

1. Nilai dari $\frac{2^{5}-2^{7}}{2^{2}}=....$

Jawab:

$\frac{2^{5}-2^{7}}{2^{2}}=\frac{2^{2}(2^{3}-2^{5})}{2^{2}}=8-32=-24$ .

2. Sederhanakanlah $\frac{a^{4}-b^{4}}{a-b}$ .

Jawab:

$\frac{a^{4}-b^{4}}{a-b}=\frac{(a^{2}+b^{2})(a^{2}-b^{2})}{a-b}=(a^{2}+b^{2})(a+b)$ .

3. Nilai $x$ dari $\sqrt[3]{8^{x+2}}=(\frac{1}{32})^{2-x}$ .

Jawab:

$\sqrt[3]{8^{x+2}}=(\frac{1}{32})^{2-x} \Rightarrow (2^{3})^{\frac{x+2}{3}}=(2^{-5})^{2-x}\Rightarrow 2^{x+2}=2^{5x-10}\Rightarrow x+2=5x-10\Rightarrow x=3$ .

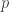4. Jika $x> 0$ dan $x\neq 1$ pada $x^{p}=\frac{\sqrt{x\sqrt{x\sqrt{x}}}}{x}$ , maka nilai $p$ adalah ….

Jawab:

Perhatikan bahwa $\sqrt{x\sqrt{x\sqrt{x}}}=\sqrt{x\sqrt{x^{\frac{3}{2}}}}=\sqrt{x^{\frac{7}{4}}}=x^{\frac{7}{8}}$ .

Sehingga persamaan menjadi

$\frac{x^{\frac{7}{8}}}{x}=x^{p}\Rightarrow x^{-\frac{1}{8}}=x^{p}\Rightarrow p=-\frac{1}{8}$ .

5. (UN Mat SMA/MA IPA 2014) Bentuk sederhana dari $(\frac{4a^{-3}b^{-5}c}{36a^{-5}b^{-3}c^{-1}})^{2}$ adalah …

Jawab:

$(\frac{4a^{-3}b^{-5}c}{36a^{-5}b^{-3}c^{-1}})^{2}=(\frac{a^{-3+5}b^{-5+3}c^{1+1}}{9})^{2}=(\frac{a^{2}b^{-2}c^{2}}{3^{2}})^{2}=(\frac{a^{2}c^{2}}{3^{2}b^{2}})^{2}=(\frac{ac}{3b})^{4}$ .

6. (UN Mat SMA/MA IPA 2014) Bentuk sederhana dari $(\frac{3a^{-2}b^{3}c^{4}}{15a^{3}b^{-5}c^{-2}})^{-1}$ adalah ….

Jawab:

$(\frac{3a^{-2}b^{3}c^{4}}{15a^{3}b^{-5}c^{-2}})^{-1}=(\frac{15a^{3}b^{-5}c^{-2}}{3a^{-2}b^{3}c^{4}})=5a^{3+2}b^{-5-3}c^{-2-4}=\frac{5a^{5}}{b^{8}c^{6}}$ .

7. (UN Mat SMA/MA IPA 2014) Bentuk sederhana dari $(\frac{3a^{-2}bc^{-3}}{24a^{5}b^{-3}c})^{-1}$ adalah ….

Jawab:

$(\frac{3a^{-2}bc^{-3}}{24a^{5}b^{-3}c})^{-1}=(\frac{24a^{5}b^{-3}c}{3a^{-2}bc^{-3}})=8a^{5+2}b^{-3-1}c^{1+3}=\frac{8a^{7}c^{4}}{b^{4}}$ .

8. (UN Mat SMA/MA IPA 2014) Bentuk sederhana dari $\frac{6}{3-2\sqrt{2}}$ adalah ….

Jawab:

$\frac{6}{3-2\sqrt{2}}=\frac{6}{3-2\sqrt{2}}.(\frac{3+2\sqrt{2}}{3+2\sqrt{2}})=\frac{6(3+2\sqrt{2})}{9-8}=18+12\sqrt{2}$ .

9. (UN Mat SMA/MA IPA 2014) Bentuk sederhana dari $\frac{9}{2\sqrt{2}-\sqrt{5}}=....$

Jawab:

$\frac{9}{2\sqrt{2}-\sqrt{5}}=\frac{9}{2\sqrt{2}-\sqrt{5}}.(\frac{2\sqrt{2}+\sqrt{5}}{2\sqrt{2}+\sqrt{5}})=\frac{9.(2\sqrt{2}+\sqrt{5})}{8-5}=3(2\sqrt{2}+\sqrt{5})$ .

10. (UN Mat SMA/MA IPA 2014) Bentuk sederhana dari $\frac{12}{3\sqrt{2}-2\sqrt{3}}$ adalah ….

Jawab:

$\frac{12}{3\sqrt{2}-2\sqrt{3}}=\frac{12}{3\sqrt{2}-2\sqrt{3}}.(\frac{3\sqrt{2}+2\sqrt{3}}{3\sqrt{2}+2\sqrt{3}})=\frac{12(3\sqrt{2}+2\sqrt{3})}{18-12}=2(3\sqrt{2}+2\sqrt{3})$ .

11. (UN Mat SMA/MA IPA 2014) Nilai dari $\frac{^{3}\log \frac{1}{9}+^{\sqrt{2}}\log 9.^{3}\log 16}{^{2}\log 10-^{2}\log 5}=....$

Jawab:

$\frac{^{3}\log \frac{1}{9}+^{\sqrt{2}}\log 9.^{3}\log 16}{^{2}\log 10-^{2}\log 5}=\frac{^{3}\log 3^{-2}+^{2^{\frac{1}{2}}}\log 3^{2}.^{3}\log 2^{4}}{^{2}\log \frac{10}{2}}=\frac{-2+\frac{2.4}{\frac{1}{2}}.^{2}\log 3.^{3}\log 2}{^{2}\log 2}=\frac{-2+16}{1}=14$ .

12. (UN Mat SMA/MA IPA 2014) Hasil dari $\frac{^{3}\log 25.^{5}\log 81-^{4}\log 2}{^{3}\log 36-^{3}\log 4}=....$ .

Jawab:

$\frac{^{3}\log 25.^{5}\log 81-^{4}\log 2}{^{3}\log 36-^{3}\log 4}=\frac{^{3}\log 5^{2}.^{5}\log 3^{4}-^{2^{2}}\log 2^{1}}{^{3}\log \frac{36}{4}}=\frac{2.4.^{3}\log 5.^{5}\log 3-\frac{1}{2}}{^{3}\log 3^{2}}=\frac{8-\frac{1}{2}}{2}=\frac{15}{4}$ .

13. Jadikanlah dalam bentuk $\sqrt{a}\pm \sqrt{b}$ dengan $a> b$ dari $\sqrt{9-\sqrt{56}}$ .

Jawab:

$\sqrt{9-\sqrt{56}}=\sqrt{9-\sqrt{4.14}}=\sqrt{7+2-2\sqrt{7.2}}=\sqrt{(\sqrt{7}-\sqrt{2})^{2}}=\sqrt{7}-\sqrt{2}$ .

14. Jadikanlah dalam bentuk $\sqrt{a}\pm \sqrt{b}$ dengan $a> b$ dari $\sqrt{5-\sqrt{21}}=....$ .

Jawab:

$\sqrt{5-\sqrt{21}}=\sqrt{5-2.\frac{1}{2}.\sqrt{21}}=\sqrt{(\frac{7}{2}+\frac{3}{2})-2.\frac{1}{2}.\sqrt{7.3}}=\sqrt{(\frac{\sqrt{7}}{\sqrt{2}}-\frac{\sqrt{3}}{\sqrt{2}})^{2}}=\frac{\sqrt{7}}{\sqrt{2}}-\frac{\sqrt{3}}{\sqrt{2}}=\frac{1}{2}(\sqrt{14}-\sqrt{6})$ .

15. (Olimpiade Sains Mat SMA/MA Porsema NU Th 2012) Nilai $x$ yang memenuhi jika $(\sqrt{3+2\sqrt{2}})^{x}-(\sqrt{3+2\sqrt{2}})^{-x}=\frac{3}{2}$ adalah ….

Jawab:

Misalkan $p=\sqrt{3+2\sqrt{2}}$ maka $p^{x}-p^{-x}=\frac{3}{2} \Rightarrow p^{x}-\frac{1}{p^{x}}=\frac{3}{2}$ .

Selanjutnya $2p^{2x}-3p^{x}-2=0 \Rightarrow (2p^{x}+1).(p^{x}-2)=0$ maka $p^{x}=-\frac{1}{2}$ atau $p^{x}=2$ .

Sehingga yang memenuhi adalah $p^{x}=(\sqrt{3+2\sqrt{2}})^{x}=2$ .

Untuk mencari $x$ kita gunakan l0garitma, yaitu $(\sqrt{3+2\sqrt{2}})^{x}=2\Rightarrow x=^{\sqrt{3+2\sqrt{2}}}\log 2$ .

Karena $\sqrt{3+2\sqrt{2}}=\sqrt{(\sqrt{2}+1)^{2}}$ , kita mendapatkan jawaban akhir yaitu $x=^{\sqrt{2}+1}\log 2$ .

16. Tunjukkan bahwa

$\sqrt{1+a(a+1)(a+2)(a+3)}=a^{2}+3a+1$
$\sqrt{16+a(a+2)(a+4)(a+6)}=a^{2}+6a+4$
$\sqrt{81+a(a+3)(a+6)(a+9)}=a^{2}+9a+9$
$\sqrt{256+a(a+4)(a+8)(a+12)}=a^{2}+12a+16$
$\sqrt{625+a(a+5)(a+10)(a+15)}=a^{2}+15a+25$
$\sqrt{n^{2}+a(a+n)(a+2n)(a+3n)}=a^{2}+3an+n^{2}$ , serta
Hitunglah nilai dari $\sqrt{1+2012.2013.2014.2015}=....$ .

Jawab:

Akan ditunjukkan no. 1 saja dan nomor yang lain untuk dicoba sebagai latihan.

Perhatikan bahwa

$\sqrt{1+a(a+1)(a+2)(a+3)}=\sqrt{1+a(a+3)(a+2)(a+1)}=\sqrt{1+(a^{2}+3a)(a^{2}+3a+2)}=\sqrt{1+(a^{2}+3a)^{2}+2(a^{2}+3a)}=\sqrt{(a^{2}+3a)^{2}+2(a^{2}+3a)+1}=\sqrt{(a^{2}+3a+1)^{2}}=a^{2}+3a+1$ .

17. Jika diketahui $a^{b}=2^{2015}-2^{2014}\: ,\: \: tentukan\: nilai\: a+b\: ?$

Jawab:

$a^{b}=2^{2015}-2^{2014}=2^{2014+1}-2^{2014+0}=2^{2014}.2^{1}-2^{2014}.2^{0}=2^{2014}\left ( 2-1 \right )=2^{2014}$ .

Jadi, nilai $\left\{\begin{matrix} a & = & 2\\ b & = & 2014 \end{matrix}\right.,\: \: sehingga\: \: a+b=2016$ .

MEDIA PEMBELAJARAN BERBASIS BLOG FARAH FABIOLA

Thursday, May 16, 2019